ResonanceMode¶
| Type: | section |
|---|---|
| Appearance: | simple |
| Excludes: | PropagatingMode, Scattering |
This section specifies a resonance mode problem. It is the aim to find pairs 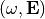 , or equivalently
, or equivalently 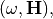 satisfying the time-harmonic Maxwell’s equations in a source-free medium.
satisfying the time-harmonic Maxwell’s equations in a source-free medium.
Special geometries
2-dimensional, straight
When passing a two-dimensional grid file grid.jcm, JCMsolve treats the geometry as infinitely extended in the  -direction. The computed eigenfields depend harmonically on
-direction. The computed eigenfields depend harmonically on  , that is
, that is
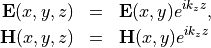
The user must fix the longitudinal component 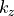 of the BlochVector.
of the BlochVector.
3-dimensional, cylindrical
When the geometry exhibits a cylinder symmetry with respect to the 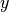 -axis, it is possible to reduce the eigenmode computation to a two dimensional problem.
-axis, it is possible to reduce the eigenmode computation to a two dimensional problem.
Let 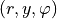 denote the cylindrical coordinates related to the Cartesian coordinates
denote the cylindrical coordinates related to the Cartesian coordinates 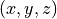 by
by
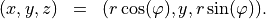
The material distribution is rotational symmetric when the permittivity tensor field  and the permeability tensor field
and the permeability tensor field 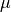 satisfy
satisfy
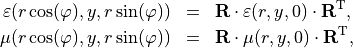
with the rotation matrix
![\begin{eqnarray*}
\TField{R} & = & \left [
\begin{array}{ccc}
\cos(\varphi) & 0 & -\sin(\varphi) \\
0 & 1 & 0 \\
\sin(\varphi) & 0 & \cos(\varphi) \\
\end{array}
\right ].
\end{eqnarray*}](_images/math/410217f6aece1b0c4f2f3692bba4b0bf66771372.png)
Hence, the device is fully described by the material distribution within the cross section 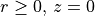 , so that
, so that JCMsolve expects a two-dimensional grid file grid.jcm.
Any eigenfield show up a symmetry with respect to the angular variable 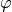 . For the electric and field it holds true that:
. For the electric and field it holds true that:
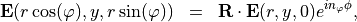
with an integer value 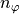 .
.
Up to a phase factor 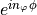 , the electric field is determined by the values within the cross section. The same holds true for other vector fields, i.e., for the magnetic field
, the electric field is determined by the values within the cross section. The same holds true for other vector fields, i.e., for the magnetic field  or the Poynting vector
or the Poynting vector 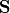 . Scalar fields such as the electromagnetic field energy density are independent of
. Scalar fields such as the electromagnetic field energy density are independent of 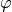 .
.
For a resonance mode computation, the user must fix the integer wave number 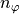 , see BlochVector.
, see BlochVector.