Port¶
| Type: | enum |
|---|---|
| Range: | Origin |
| Default: | Origin |
| Appearance: | simple |
, or
| Type: | int |
|---|---|
| Range: | [1, 2147483647] |
A polygon has a point-Port (globally oriented) at its vertices and tangential ports at the midpoints of its segments. Further, a polygon as the default port Origin which coincides with the origin of the global coordinate-system.
The port ordering is as follows, where 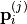 denotes the
denotes the 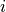 -th point of the
-th point of the 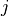 -th polygonal chain with
-th polygonal chain with 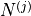 points and
points and 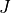 is the number of polygonal chains:
is the number of polygonal chains:
| Number | Name | Position | Type | Coordinate System |
|---|---|---|---|---|
| 1 | 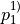 |
point | ![x'=[1, 0], y'=[0, 1]](_images/math/1072fb7b0f6ffa31760363593858bdd8b9ee4fb8.png) |
|
| … | … | point | … | |
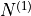 |
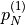 |
point | ![x'=[1, 0], y'=[0, 1]](_images/math/1072fb7b0f6ffa31760363593858bdd8b9ee4fb8.png) |
|
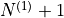 |
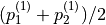 |
tangential | 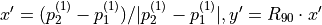 |
|
| … | tangential | … | ||
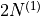 |
… | 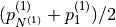 |
tangential | 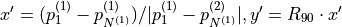 |
| … | … | … | … | … |
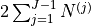 |
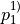 |
point | ![x'=[1, 0], y'=[0, 1]](_images/math/1072fb7b0f6ffa31760363593858bdd8b9ee4fb8.png) |
|
| … | … | point | … | |
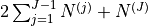 |
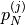 |
point | ![x'=[1, 0], y'=[0, 1]](_images/math/1072fb7b0f6ffa31760363593858bdd8b9ee4fb8.png) |
|
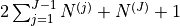 |
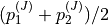 |
tangential | 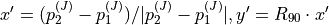 |
|
| … | tangential | … | ||
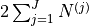 |
… | 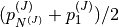 |
tangential | 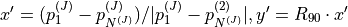 |
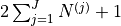 |
Origin | ![[0, 0]](_images/math/d29d2f7c1cea4b5381dadcbd9ab0226cb9189a30.png) |
point | ![x'=[1, 0], y'=[0, 1]](_images/math/1072fb7b0f6ffa31760363593858bdd8b9ee4fb8.png) |