RelPermittivity¶

Type:	2-Tensor, or section
Range:	[v_1, …, v_9]
Default:	[1.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 1.0]
Appearance:	simple

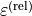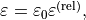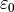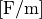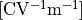Specifies the relative permittivity $\TField{\varepsilon}^{(\mathrm{rel})}$ . The relative permittivity is dimensionless. It defines the permittivity as $\varepsilon=\varepsilon_0 \TField{\varepsilon}^{(\mathrm{rel})},$ where $\varepsilon_0$ is the vacuum permittivity in units farads per meter, $\units{F/m}$ (which equals to units coulomb per volt per meter, $\units{CV^{-1}m^{-1}}$ ). 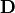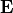The permittivity $\varepsilon$ relates the electric displacement $\TField{D}$ to the electric field strength $\TField{E}$ ,

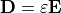
$\begin{align*} \TField{D} &=\varepsilon \TField{E} \end{align*}$

For the extension to bi-anistropic materials see RelBiPermittivity.

A constant relative permittivity can be defined by assigning a rank-2 tensor:

Material {
  # defines a constant relative permittivity
  RelPermittivity =
      [..., ..., ...
       ..., ..., ...
       ..., ..., ...]
}

Assign a scalar for an isotropic relative permittivity:

Material {
  ...
  RelPermittivity = 2.25
}

For more general cases, the relative permittivity may be given as a section in order to deal with space, time, frequency and parameter dependent definitions:

# define the relative permittivity as a section
RelPermittivity {
  Python {...}
  PhotoElasticCorrection { ... }
  ThermoOpticalCorrection { ... }
  ...
}

Field definitions within the section RelPermittivity are summed up. Consult the subsequent sections to see which types of field definitions are allowed.

Note

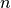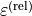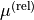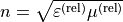The refractive index (index of refraction, $n$ ) of an optical medium relates to the relative permittivity $\TField{\varepsilon}^{(\mathrm{rel})}$ and relative permeability $\TField{\mu}^{(\mathrm{rel})}$ as $n=\sqrt{\TField{\varepsilon}^{(\mathrm{rel})} \TField{\mu}^{(\mathrm{rel})}}$ . In most cases, 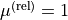$\TField{\mu}^{(\mathrm{rel})}=1$ . Therefore, e.g., for an isotropic material with refractive index 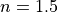$n=1.5$ , the relative permittivity is specified as RelPermittivity = 2.25.

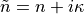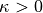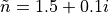Lossy materials can be modeled using a complex refractive index, $\tilde{n}=n+i\kappa$ , with $\kappa>0$ , e.g., $\tilde{n}=1.5+0.1i$ . In this example, a complex relative permittivity is specified: RelPermittivity = 2.24+0.3i. (Please note the sign convention, where a positive $\kappa$ relates to absorption, c.f., TimeHarmonic.)