NonLinearSusceptibility¶
| Type: | Matrix<complex> |
|---|---|
| Range: | [v_11, …, v_1j; …; v_i1, …; v_ij], i<=3, j<=6 |
| Default: | -/- |
| Appearance: | simple |
, or
| Type: | 3-Tensor |
|---|---|
| Range: | [v_1, …, v_27] |
, or
| Type: | 4-Tensor |
|---|---|
| Range: | [v_1, …, v_81] |
, or
| Type: | Dictionary<complex> |
|---|---|
| Range: | [(-inf-infj), (inf+infj)] |
The NonLinearSusceptibility represents a nonlinear susceptibility tensor 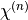 used to describe various nonlinear polarization effects in materials, where
used to describe various nonlinear polarization effects in materials, where 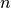 indicates the order of nonlinearity.
indicates the order of nonlinearity.
This tensor is used to model a wide range of nonlinear optical processes, including:
- Second-harmonic generation (SHG)
- Third-harmonic generation (THG)
- Sum-frequency generation (SFG)
- Difference-frequency generation (DFG)
- Kerr-type nonlinearities
driven by one or more electric fields.
JCMsuite supports a flexible input format and automatic inference of the tensor rank when using dictionary input.
The susceptibility tensor Chi can be specified in multiple formats:
- Full Tensor Representation:
Provided as a rank-3 or rank-4 tensor supplying all tensor entries (see cf. Data Structure for format).
JCMsuitewill determine the order of the nonlinearity from the tensor rank. No symmetry is assumed, and all the tensor components have to be provided.
Example:
Chi = [0, 0, 0, 0, 0, 7.4e-10, 0, 7.4e-10, 0, 0, 0, 7.4e-10, 0, 0, 0, 7.4e-10, 0, 0, 0, 7.4e-10, 0, 7.4e-10, 0, 0, 0, 0, 0 ]
- Dictionary Representation:
A sparse representation where only non-zero tensor components are given. Keys are index tuples (e.g.,
ijkorijkl), and values are the corresponding tensor components. No symmetry is assumed, and all non-zero tensor components have to be provided.
Example:
Chi = [ 123: 740.0e-12, 132: 740.0e-12, 231: 740.0e-12, 213: 740.0e-12, 312: 740.0e-12, 321: 740.0e-12]
- Reduced Kleinman Representation (for SHG):
A compact 3×6 matrix form assuming Kleinman symmetry. Only applicable for second-order nonlinearities (e.g., SHG). Supports automatic mapping to the full 3-index tensor form.
Example:
Chi = [ 0 0 0 370.0e-12 0 0 0 0 0 0 370.0e-12 0 0 0 0 0 0 370.0e-12 ]