Chiral Quantities¶
The optical chirality 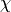 is a measure of the local density of chirality of the electromagnetic field [1].
It satisfies the continuity equation
is a measure of the local density of chirality of the electromagnetic field [1].
It satisfies the continuity equation 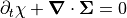 in isotropic
homogeneous media. For monochromatic, i.e. time-harmonic, fields the optical chirality
in isotropic
homogeneous media. For monochromatic, i.e. time-harmonic, fields the optical chirality 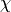 is proportional
to the helicity of light and the optical chirality flux
is proportional
to the helicity of light and the optical chirality flux 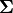 is proportional to the spin angular momentum [2].
is proportional to the spin angular momentum [2].
In its generalized time-harmonic form, the optical chirality density 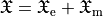 and the optical chirality flux density
and the optical chirality flux density 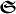 satisfy a continuity equation valid in arbitrary, i.e. bi-anisotropic, space [3] :
satisfy a continuity equation valid in arbitrary, i.e. bi-anisotropic, space [3] :
![\begin{eqnarray}
2 i \omega (\mathfrak{X}_\text{e} - \mathfrak{X}_\text{m}) + \boldsymbol{\nabla} \cdot \boldsymbol{\mathfrak{S}} = -\frac{1}{4} \left[ \VField{J}^* \cdot \left( \boldsymbol{\nabla} \times \boldsymbol{\VField{E}}\right) + \boldsymbol{\VField{E}} \cdot \left( \boldsymbol{\nabla} \times \VField{J}^*\right) \right],
\label{eq:chCont}
\end{eqnarray}](_images/math/da4156acb515038afa58cf50b0a0572407b3ec15.png)
where 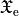 is the ElectricChiralityDensity,
is the ElectricChiralityDensity, 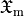 is the MagneticChiralityDensity and
is the MagneticChiralityDensity and 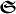 is the ElectromagneticChiralityFluxDensity.
is the ElectromagneticChiralityFluxDensity.
ElectricChiralityDensity
The electric part of the optical chirality density
is accessible as ElectricChiralityDensity within
JCMsuiteand defined as
In isotropic media, this reduces to
which is accessible as ElectricChiralityDensity. This quantity
can be computed numerically more accurate and faster. However, it only satisfies the continuity equation
in isotropic media.
MagneticChiralityDensity
The magnetic part of the optical chirality density in
is accessible as AnisotropicMagneticChiralityDensity and defined as
In isotropic media, this reduces to
which is accessible as MagneticChiralityDensity. This quantity
can be computed numerically more accurate and faster. However, it only satisfies the continuity equation
in isotropic media.
For homogeneous isotropic lossless media, the real part of the sum of the ElectricChiralityDensity and the MagneticChiralityDensity is the time-harmonic optical chirality density 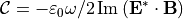 used by many authors [4].
used by many authors [4].
ElectromagneticChiralityFluxDensity
The optical chirality flux density in
is accessible as ElectromagneticChiralityFluxDensity and defined as
Due to Maxwell’s equations, this flux density can be rewritten as
Its real part is proportional to the spin angular momentum, whereas its imaginary part has no physical significance.
Integrated Chiral Quantities¶
In order to obtain measurable quantities, the continuity equation for chiral quantities 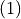 can be integrated. This yields a conservation law analogous to Poynting’s theorem which states the conservation of electromagnetic energy. The extinction of energy occurs due to scattering and absorption. The extinction of optical chirality
can be integrated. This yields a conservation law analogous to Poynting’s theorem which states the conservation of electromagnetic energy. The extinction of energy occurs due to scattering and absorption. The extinction of optical chirality 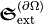 is due to scattering
is due to scattering 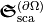 and conversion
and conversion 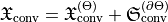 which takes place in volumes
which takes place in volumes 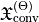 or at interfaces
or at interfaces 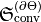 [3].
[3].
The conservation of optical chirality reads as
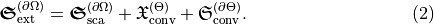
Conversion
- Volume Conversion
The conversion of optical chirality in volumes is accessible by performing the PostProcess DensityIntegration with the OutputQuantity ElectricChirality and MagneticChirality. Analogous to the case of energy absorption, the physically relevant part is
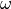 -times the imaginary part:
-times the imaginary part: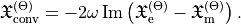
- ElectromagneticChiralityConversionFlux
- In contrast to energy, optical chirality is not conserved in media with spatial dependent material parameters, especially on interfaces of piecewise-constant materials. The conversion of optical chirality occurring at interfaces is accessible by performing the PostProcess FluxIntegration with the OutputQuantity ElectromagneticChiralityConversionFlux. The physically relevant part
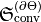 in
in 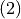 is the real part of this quantity.
is the real part of this quantity.
Note
The InterfaceType has to be set to DomainInterfaces.
ScatteredElectromagneticChiralityFlux
The optical chirality flux of the scattered field is accessible by performing the PostProcess FluxIntegration with the OutputQuantity ScatteredElectromagneticChiralityFlux. The physically relevant partin
is the real part of this quantity.
Note
The InterfaceType is automatically set to ExteriorDomain.
ExtinctionElectromagneticChiralityFlux
The extinction of optical chirality is accessible by performing the PostProcess FluxIntegration with the OutputQuantity ExtinctionElectromagneticChiralityFlux. The physically relevant partin
is the real part of this quantity.
Note
The InterfaceType is automatically set to ExteriorDomain.
Up to numerical inaccuracies, this quantity should equal the sum of the scattered chirality 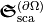 and the chirality conversion obtained from volumes
and the chirality conversion obtained from volumes 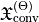 and interfaces
and interfaces 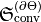 .
If this is not the case, increase the Precision and/or FiniteElementDegree and/or MaximumSideLength of your simulation.
.
If this is not the case, increase the Precision and/or FiniteElementDegree and/or MaximumSideLength of your simulation.
Bibliography
| [1] | Yiqiao Tang and Adam E. Cohen. Optical chirality and its interaction with matter. Physical review letters, 104(16):163901, 2010. |
| [2] | Konstantin Y. Bliokh and Franco Nori. Characterizing optical chirality. Physical Review A, 83(2):021803, 2011. |
| [3] | (1, 2) Philipp Gutsche, Lisa V. Poulikakos, Martin Hammerschmidt, Sven Burger, and Frank Schmidt. Time-harmonic optical chirality in inhomogeneous space. In SPIE OPTO, Vol.9756, pages 97560X. International Society for Optics and Photonics, 2016. |
| [4] | Martin Schäferling, Daniel Dregely, Mario Hentschel, and Harald Giessen. Tailoring enhanced optical chirality: design principles for chiral plasmonic nanostructures. Physical Review X, 2(3):031010, 2012. |
![\begin{eqnarray*}
\mathfrak{X}_\text{e} = \frac{1}{8} \left[ \boldsymbol{\VField{D}}^* \cdot \left( \boldsymbol{\nabla} \times \boldsymbol{\VField{E}}\right) + \boldsymbol{\VField{E}} \cdot \left( \boldsymbol{\nabla} \times \boldsymbol{\VField{D}}^*\right) \right].
\end{eqnarray*}](_images/math/21fecc04204c60058cd7c71960ffad4065c59670.png)
![\begin{eqnarray*}
\widetilde{\mathfrak{X}_\text{e}} = \frac{1}{8} i \omega \left[ \boldsymbol{\VField{D}}^*\cdot \boldsymbol{\VField{B}} - \left(\varepsilon \boldsymbol{\VField{B}}\right)^* \cdot \boldsymbol{\VField{E}} \right]
\end{eqnarray*}](_images/math/9edc2890bcbd8e7350d72a3033359e0c0dcf872f.png)
![\begin{eqnarray*}
\mathfrak{X}_\text{m} = \frac{1}{8} \left[ \boldsymbol{\VField{H}}^* \cdot \left( \boldsymbol{\nabla} \times \boldsymbol{\VField{B}}\right) + \boldsymbol{\VField{B}} \cdot \left( \boldsymbol{\nabla} \times \boldsymbol{\VField{H}}^*\right) \right].
\end{eqnarray*}](_images/math/c6f0cc3fde34e5dbcfc64e6457a29dd4be0f9bb5.png)
![\begin{eqnarray*}
\widetilde{\mathfrak{X}_\text{m}} = \frac{1}{8} i \omega \left[ \boldsymbol{\VField{D}}^* \cdot \boldsymbol{\VField{B}} - \boldsymbol{\VField{H}}^* \left(\mu \boldsymbol{\VField{D}}\right) \right],
\end{eqnarray*}](_images/math/b07b281525fe4d1de7087fe21816aa2138adbc19.png)
![\begin{eqnarray*}
\boldsymbol{\mathfrak{S}} = \frac{1}{4} \left[ \boldsymbol{\VField{E}} \times \left( \boldsymbol{\nabla} \times \boldsymbol{\VField{H}}^*\right) - \boldsymbol{\VField{H}}^* \times \left( \boldsymbol{\nabla} \times \boldsymbol{\VField{E}}\right) \right].
\end{eqnarray*}](_images/math/273e3f227e42e8fae1352244fc87f99bde9a1eb4.png)
![\begin{eqnarray*}
\boldsymbol{\mathfrak{S}} = \frac{1}{4} i \omega \left[\boldsymbol{\VField{E}} \times \boldsymbol{\VField{D}}^* - \boldsymbol{\VField{H}}^* \times \boldsymbol{\VField{B}} \right].
\end{eqnarray*}](_images/math/8145372d129646232c3800a6e22b69f6c25adef5.png)