PropagatingMode¶

Type:	section
Appearance:	simple
Excludes:	ResonanceMode, Scattering

This section specifies a propagating mode problem. This type of problem is also called waveguide problem.

The angular frequency 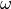$\omega$ is a fixed parameter $\omega_0$ of the problem and one defines the vacuum wavelength 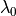$\lambda_0$ and k-vector 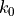$k_0$ by

$\begin{eqnarray*} k_0 & = & \frac{\omega_0}{c} = \frac{2\pi}{\lambda_0}, \end{eqnarray*}$

where $c$ is the speed of light in the vacuum.

A waveguide geometry is characterized by a special axis, the waveguide or longitudinal direction, with a dimension much larger than the cross section diameter and measuring a huge number of wavelengths 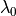$\lambda_0$ . The waveguide is then modeled as infinitely prolonged. On a macroscopic scale the waveguide axis need not to be straight. JCMsolve can take bending effects into account, c.f., parameter AxisPositionX. Furthermore, the waveguide geometry is allowed to be twisted along the waveguide axis (parameter Twist, see also [1]).

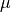In the following we only discuss the straight waveguide with a longitudinal axis along the $z$ -direction. The coordinate system is chosen such that the geometry exhibits an invariance in the $z$ -direction, that is, the permittivity tensor $\TField{\varepsilon}$ and the permeability tensor $\mu$ do not depend on the longitudinal direction $z$ .

It is the aim to find propagating modes which solve Maxwell equations in source-free media and which depend harmonically on $z$ , in the sense that

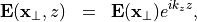
$\begin{eqnarray*} \VField{E}(\pvec{x}_\perp, z) & = & \VField{E}(\pvec{x}_\perp) e^{ik_z z}, \end{eqnarray*}$

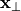where $k_z \in \cnum$ is the propagation constant and $\pvec{x}_\perp$ denotes the cross-section coordinates $x, y$ .

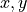Introducing the operator

$\begin{eqnarray*} \nablakz & = & \left ( \begin{array}{c} \partial_x \\ \partial_y \\ i k_z \end{array} \right) \end{eqnarray*}$

The time harmonic Maxwell’s equations of second order, see parent section, now read as

$\begin{eqnarray*} \curlkz \mu^{-1} \curlkz \VField{E}(\pvec{x}_\perp) - \omega^2 \TField{\varepsilon} \VField{E}(\pvec{x}_\perp) & = & 0 \end{eqnarray*}$

with analogue equations for the magnetic field.

The dependency on the $z$ -coordinate has disappeared and the problem is posed on the cross-section only.

The above eigenmode equation has the structure of an eigenvalue problem: One seeks pairs 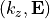$(k_z, \VField{E})$ of the propagating constant and the field distribution.

Traditionally, the eigenvalue is not given as the propagation constant 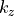$k_z$ but in the form of an effective refractive index

$\begin{eqnarray*} n_{\mathrm{eff}} & = & k_z/k_0. \end{eqnarray*}$

Bibliography

[1]

Nicolet, F. Zolla, Y. Ould Agha, S. Guenneau, (2008) Geometrical transformations and equivalent materials in computational electromagnetism, COMPEL: The International Journal for Computation and Mathematics in Electrical and Electronic Engineering, Vol. 27 Iss: 4, pp.806 - 819, Geometrical transformations and equivalent materials in computational electromagnetism.