PCELeastSquare¶
Purpose¶
The goal of the driver is to perform a global sensitivity analysis of model parameters 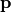 reconstructed from a minimization of the regression standard error.
The regression standard error with respect to an observed target vector
reconstructed from a minimization of the regression standard error.
The regression standard error with respect to an observed target vector
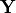 (e.g. a measurement) is defined as
(e.g. a measurement) is defined as
![\text{RSE}(\mathbf{p}) = \sqrt{[\mathbf{Y} - \mathbf{y}(\mathbf{p})]^T G^{-1} [\mathbf{Y} - \mathbf{y}(\mathbf{p})]/\text{DOF}},](_images/math/d866eac79b16544e814e259d7de136798560f5db.png)
where 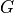 is the covariance matrix of the target vector entries and
is the covariance matrix of the target vector entries and
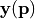 it the model vector, which depends on the
parameter values
it the model vector, which depends on the
parameter values 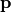 .
The number of degrees of freedom DOF is the difference between the length of the
target vector
.
The number of degrees of freedom DOF is the difference between the length of the
target vector 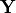 and the length of the parameter vector
and the length of the parameter vector
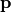 . If the number of degrees of freedom is negative, we set DOF=1.
The regression standard error is often also denoted as noise level or standard deviation STD. The square of the RSE is the the mean squared error MSE.
. If the number of degrees of freedom is negative, we set DOF=1.
The regression standard error is often also denoted as noise level or standard deviation STD. The square of the RSE is the the mean squared error MSE.
The driver performs a global polynomial chaos expansion (PCE) of all entries of the model vector 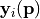 .
.
Depending on the defined random distribution of each parameter (see parameter distribution), PCE uses different polynomials to obtain a good 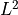 convergence.
convergence.
| Distribution of random variable | Polynomials
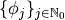 |
|---|---|
| Uniform | Legendre |
| Gauss | Hermite |
| Gamma | Laguerre |
| Beta | Jacobi |
Using the default setting, the number of of expansion terms is chosen automatically based on a variance analysis of the model vector 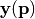 .
.
The PCE can be used to predict the RSE and its derivatives 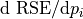 for any parameter vector
for any parameter vector 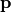 . Predictions can be computed by calling study.predict().
. Predictions can be computed by calling study.predict().
It is possible to retrieve the covariances between the model parameters at the found minimum of the RSE (see Driver-specific Information). The paramter covariance matrix 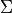 gives an estimate of the uncertainties of the reconstructed parameters under the assumption that the model vector entries
gives an estimate of the uncertainties of the reconstructed parameters under the assumption that the model vector entries 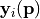 depend linearly on
depend linearly on 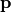 . The standard deviations of the parameter value
. The standard deviations of the parameter value 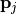 are given as
are given as 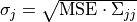 .
.
The PCE typically contains also higher order dependencies of 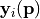 around the minimium of the RSE.
In order to determine the parameter uncertainties including non-linear terms, it is possible to sample the probability distribution of the reconstructed parameters using a Markov chain Monte Carlo sampling (study.run_mcmc()). For this sampling, it is also possible to define more complex error models (see error_model). After a MCMC sampling, the reconstructed parameter values are determined by the median value of the probability distribution. The lower uncertainty is given by the 16% quantile of the distribution and the upper uncertainty as the 84% quantile.
around the minimium of the RSE.
In order to determine the parameter uncertainties including non-linear terms, it is possible to sample the probability distribution of the reconstructed parameters using a Markov chain Monte Carlo sampling (study.run_mcmc()). For this sampling, it is also possible to define more complex error models (see error_model). After a MCMC sampling, the reconstructed parameter values are determined by the median value of the probability distribution. The lower uncertainty is given by the 16% quantile of the distribution and the upper uncertainty as the 84% quantile.
Usage Example¶
addpath(fullfile(getenv('JCMROOT'), 'ThirdPartySupport', 'Matlab'));
client = jcmwave_optimizer_client();
% Definition of the search domain
domain = {
struct('name','m', 'type','continuous', 'domain',[-5,5]),...
struct('name','b', 'type','continuous', 'domain',[0,10])...
};
% Creation of the study object with study_id 'example'
study = client.create_study('domain',domain, ...
'driver','PCELeastSquare',...
'name','PCELeastSquare example', ...
'study_id','PCELeastSquare_example');
% Generate some randomized data for a linear fit
rand("seed", 1);
N = 50; %number of datapoints
X = sort(10 * rand(1,N)); %random x-values
m0 = -0.5; %slope
b0 = 5; %offset
f0 = 0.5; % Y-proportional error
Y = m0 * X + b0; %data points
% add error proportional to Y
Y = Y + f0 * abs(Y) .* (2*rand(1,N)-1);
% add error independent of Y with mean 0.1 and and std deviation 0.5
Yerr = 0.1 + 0.5 * rand(1,N);
Y = Y + Yerr .* (2*rand(1,N)-1);
% Definition of the objective function including derivatives
function obs = objective(sample)
pause(2.0); % makes objective expensive
m = sample.m;
b = sample.b;
obs = study.new_observation();
%objective
obs = obs.add(m*X+b);
%derivative w.r.t. m
obs = obs.add(X, 'm');
%derivative w.r.t. b
obs = obs.add(0*X+1, 'b');
end
% Set study parameters
study.set_parameters('target_vector',Y, 'uncertainty_vector', Yerr);
% Run the minimization
while(not(study.is_done))
sug = study.get_suggestion();
obs = objective(sug.sample);
study.add_observation(obs, sug.id);
end
% Least square error estimate
driver_info = study.driver_info();
min_params = driver_info.predicted_min_params;
cov = driver_info.parameter_covariance;
MSE = driver_info.MSE; %mean squared error of residuum at minimum
err = sqrt(MSE*diag(cov)); %error estimate
fprintf('\nError estimates of least square minimization');
fprintf("\nm = %0.3f +/- %0.3f",min_params.m,err(1));
fprintf("\nb = %0.3f +/- %0.3f",min_params.b,err(2));
% The least square estimates are based on the uncertainty vector
% and the linear approximation of the model vector y(p).
% A Markov chain Monte Carlo (MCMC) sampling allows to determine
% the probability distribution of the model parameters including non-linear
% terms and a more realistic error model (see parameters section for details).
study.set_parameters(...
'error_model','sqrt(err_cov^2 + y_model^2 * exp(2*log_f))',...
'error_model_parameter_distribution',{...
struct('name','log_f','distribution','uniform','domain',[-10,1])...
}...
);
% The MCMC sampling with a more realistic error model gives more
% accurately reconstructed parameters.
mcmc_result = study.run_mcmc();
%MCMC sampling results: histograms and 16%,50%,84% quantiles
figure(2);
hist(mcmc_result.samples(:,1));
title_str = sprintf(['m: median %0.2f, lower uncertainty %0.2f ' ...
'upper uncertainty %0.2f'], mcmc_result.medians(1),...
mcmc_result.lower_uncertainties(1),mcmc_result.upper_uncertainties(1));
title(title_str);
figure(3);
hist(mcmc_result.samples(:,2));
title_str = sprintf(['m: median %0.2f lower uncertainty %0.2f ' ...
'upper uncertainty %0.2f'], mcmc_result.medians(2),...
mcmc_result.lower_uncertainties(2),mcmc_result.upper_uncertainties(2));
title(title_str);
Parameters¶
The following parameters can be set by calling, e.g.
study.set_parameters('example_parameter1',[1,2,3], 'example_parameter2',true);
| max_iter (int): | Maximum number of evaluations of the objective function (default: inf) |
|---|
| max_time (int): | Maximum run time in seconds (default: inf) |
|---|
| num_parallel (int): | |
|---|---|
| Number of parallel observations of the objective function (default: 1) | |
| distribution (list): | |
|---|---|
Definition of random distribution for each parameter in the format of a list. All continuous parameters with unspecified distribution are assumed to be uniformely distributed in the parameter domain. Fixed and discrete parameters are not random parameters. The value of discrete parameters defaults to the first listed value. (default: None)
|
|
| sampling_strategy (string): | |
|---|---|
| Sampling strategy of parameter values. standard: Sampler for cartesian product samples of given parameters under algebraic constraints. WLS: Sampler for weighted Least-Squares sampling as described by Cohen and Migliorati. (default: WLS) (options: [‘standard’, ‘WLS’]) | |
| polynomial_degree (int): | |
|---|---|
| Maximum degree of the polynomial chaos expansion. Can be also a list of degrees for every parameter. If not set, the polynomial degree is iteratively adapted. (default: None) | |
| limit_polynomial_degree (int): | |
|---|---|
| Maximum sum of polynomial degree of the chaos expansion. (default: 2147483647) | |
| optimization_step (int): | |
|---|---|
| Number of iterations before the polynomial degrees of the expansion are optimized. Only applies if the polynomial degree is determined automatically (polynomial_degree=None). (default: 10) | |
| optimization_step_max (int): | |
|---|---|
| Maximum number of iterations after which the polynomial degrees of the expansion are optimized. Only applies if the polynomial degree is determined automatically (polynomial_degree=None). (default: 1000) | |
| pce_update_step (int): | |
|---|---|
| Number of iterations before the PCE is updated from the samples drawn so far. At each update, e.g. the values of the Sobol coefficients are updated. (default: 5) | |
| num_test_samples (int): | |
|---|---|
| Number of samples that are drawn in order to estimate the prediction error of the PCE. (default: 10) | |
| min_prediction_error (float): | |
|---|---|
| Stopping criterium. Minimum error of the prediction of the polynomial chaos expansion for the last 5 aqcuisitions. (default: 1e-06) | |
| target_cond (float): | |
|---|---|
| Target condition number of the information matrix. Only applies if the polynomial degree is determined automatically (polynomial_degree=None). (default: 500) | |
| target_vector (list): | |
|---|---|
Vector of observations 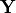 . (default: None) . (default: None) |
|
| covariance_matrix (matrix): | |
|---|---|
Covariance matrix 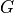 .
For a simple least-square minimization, .
For a simple least-square minimization, 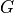 is the
identity matrix.
For measurements with different uncertainties is the
identity matrix.
For measurements with different uncertainties 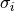 , ,
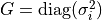 . If not specified, . If not specified, 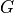 is the identity matrix. (default: None)
is the identity matrix. (default: None) |
|
| uncertainty_vector (list): | |
|---|---|
Defines the vector of measurement uncertainties
![\mathbf{s} = [\sigma_1,\sigma_2\dots]^T](_images/math/5f2f2ee0107f7fa195913a1ce88111690e4bc1f8.png) of the target vector
of the target vector 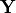 .
Accordingly, the covariance matrix is set to .
Accordingly, the covariance matrix is set to
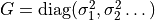 . (default: None) . (default: None) |
|
| error_model (string): | |
|---|---|
String defining error of measurement
|
|
| error_model_parameter_distribution (list): | |
|---|---|
Definition of random distribution for each parameter of the error model in the format of a list. For an example, see the documentation of error_model. (default: []) |
|
Driver-specific Information¶
A struct with following parameters can be retrieved by calling
study.driver_info().
| sobol_indices: | Dictionary mapping the names of Sobol indices (e.g. x1_x3) to the list of the corresponding parameter indices (e.g. [1,3]). |
|---|
| sobol_coefficients: | |
|---|---|
| Dictionary mapping the name of the Sobol indices (e.g. x1_x3) to the value of the Sobol coefficients. | |
| input_covariance: | |
|---|---|
Covariance matrix between entries of the vectorial input function 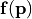 , i.e. , i.e. ![C_ij = \mathbb{E}\left[(f_i(\mathbf{p})-\overline{f}_i)(f_j(\mathbf{p})-\overline{f}_j)\right]](_images/math/c5a38ea82674a5ae8aed2d92ce0344ad813452c7.png) |
|
| predicition_error: | |
|---|---|
| Maximal predicion error of test data. | |
| num_expansion_terms: | |
|---|---|
| Number of PCE expansion terms. | |
| parameter_covariance: | |
|---|---|
Covariance matrix 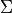 of the parameters at the sampling point with minimal discrepancy. The uncertainty of the parameter of the parameters at the sampling point with minimal discrepancy. The uncertainty of the parameter 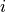 is given as is given as 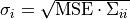 . . |
|
| MSE: | The mean squared error MSE is the square of the regression standarderror (RSE). It is given as the residual sum of squares divided by the degrees of freedom (DOF), i.e. the length of the target vector M minus the number of parameters N: MSE=RSS/(M-N). |
|---|
| predicted_min_params: | |
|---|---|
| Predicted parameter values with minimal RSE | |
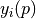 ) and the square root of the diagonal entry of the covariance matrix
) and the square root of the diagonal entry of the covariance matrix 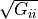 ). Other parameters with random distributions must be defined in the parameter “error_model_parameter_distribution”. The model error
). Other parameters with random distributions must be defined in the parameter “error_model_parameter_distribution”. The model error 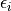 is used in the MCMC sampling to define the log likelihood as
is used in the MCMC sampling to define the log likelihood as ![ll = -0.5*\sum_i[(Y_i-y_i(p))^2/\epsilon_i^2 + \log(\epsilon_i^2)]](_images/math/80138fd156416977ddde6594746f4edf70750af7.png) .If not specified, the error model is
.If not specified, the error model is