Nanosphere¶
This tutorial example simulates light scattering off a spherical particle above a substrate.
The particle is illuminated with plane waves at oblique incidence, with S- and P-polarization.
JCMsuite computes the near-field solution.
Post-processes are used to compute absorption and scattering cross-sections, and to export field profiles.
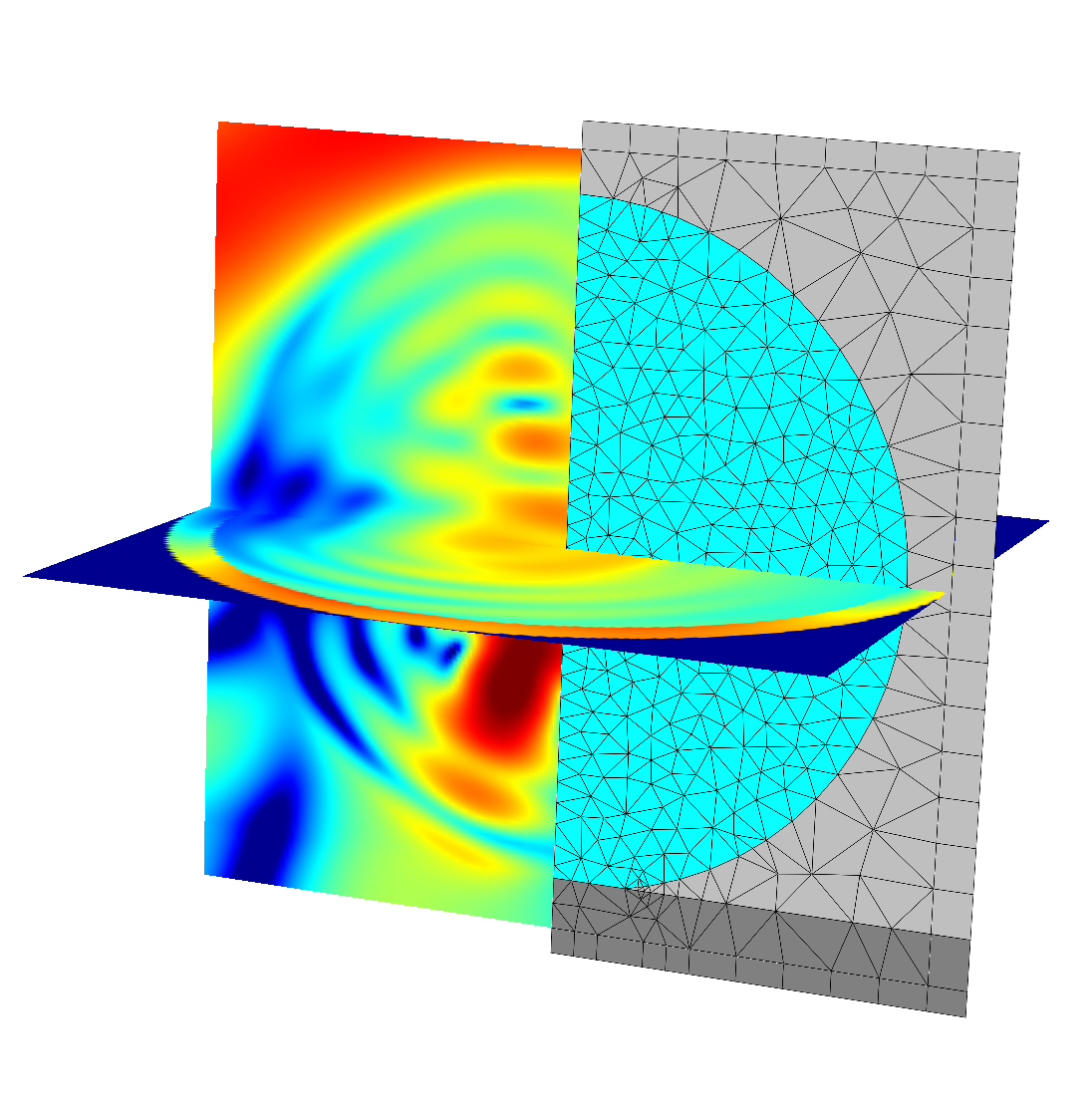
Near field intensity (pseudo-color, log-scale) in two cross-sections and triangular mesh of the geometry.¶
Definition of the geometry:
layout.jcm [ASCII]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
Layout2D { UnitOfLength = 1e-09 MeshOptions { MaximumSideLength = 100 } CoordinateSystem = Cylindrical BoundaryConditions { Boundary { Direction = All Class = Transparent } } Objects { Parallelogram { Name = "CD" Height = 900 Width = 450 Port = West GlobalPosition = [0 0] DomainId = 1 Priority = ComputationalDomain } CircleSector { Radius = 400 AngleRange = [-90 90] GlobalPosition = [0 0] DomainId = 2 Priority = 1 RefineAll = 4 MeshOptions { MaximumSideLength = 50 } } Parallelogram { Height = 900 Width = 450 Port = North Alignment { Parent { Domain = "CD" Port = South } Displacement = [-0 -60] Orientation = AntiParallel } DomainId = 3 Priority = 2 } } }
The computational domain is defined by a parallelogram in the x-y-plane. In line 6 the coordinate system is chosen which defines the y-axis as rotational symmetry axis. The sphere is defined by a (rotated) circle sector (lines 23-33), and the substrate is defined by a (rotated) parallelogram.
The refractive indices, resp. relative permittivities, of the various geometrical domains are defined here:
materials.jcm [ASCII]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Material { DomainId = 1 RelPermittivity = 1 RelPermeability = 1 } Material { DomainId = 2 RelPermittivity = (8.99, 0.6) RelPermeability = 1 } Material { DomainId = 3 RelPermittivity = 2.25 RelPermeability = 1 }
The illumination with two independent, S- and P-polarized plane waves is defined in the following:
sources.jcm [ASCII]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
SourceBag { Source { ElectricFieldStrength { PlaneWave { Lambda0 = 4e-07 ThetaPhi = [20 0] Incidence = FromAbove 3DTo2D = yes SP = [1 0] } } } } SourceBag { Source { ElectricFieldStrength { PlaneWave { Lambda0 = 4e-07 ThetaPhi = [20 0] Incidence = FromAbove 3DTo2D = yes SP = [0 1] } } } }
Project type, accuracy settings and several post-processes are defined in the project file:
project.jcmp [ASCII]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49
Project { Electromagnetics { TimeHarmonic { Scattering { FieldComponents = Electric Accuracy { FiniteElementDegree = 3 } } } } } PostProcess { DensityIntegration { FieldBagPath = "project_results/fieldbag.jcm" OutputFileName = "project_results/energy.jcm" OutputQuantity = ElectricFieldEnergy } } PostProcess { FluxIntegration { FieldBagPath = "project_results/fieldbag.jcm" OutputFileName = "project_results/scattered_energy_flux.jcm" OutputQuantity = ElectromagneticFieldEnergyFlux InterfaceType = ExteriorDomain } } PostProcess { ExportFields { FieldBagPath = "project_results/fieldbag.jcm" OutputFileName = "project_results/c_xy.jcm" Cartesian { GridPointsX = [-447.5e-9 : 5e-9 : 450e-9] GridPointsY = [-450.0e-9 : 5e-9 : 450e-9] GridPointsZ = 0 } } } PostProcess { ExportFields { FieldBagPath = "project_results/fieldbag.jcm" OutputFileName = "project_results/c_xz.jcm" Cartesian { GridPointsX = [-447.5e-9 : 5e-9 : 450e-9] GridPointsZ = [-450.0e-9 : 5e-9 : 450e-9] GridPointsY = 0 } } }
The density integration post-process can be used to compute the absorption cross-section.
The flux integration post-process can be used to compute the scattering cross-section.
(Alternatively, also far-field computation / Fourier transform post-process can be used for
obtaining angular dependent scattering amplitudes.)
ExportFields post-processes are used for visualization purposes in this case.
The data_analysis folder contains also a script where geometrical, material, source, and computational parameters can be set, and where a wavelength scan is performed, yielding computation of the wavelength dependent absorption and scattering cross-sections (with corresponding template files layout.jcmt, sources.jcmt, materials.jcmt, project.jcmpt).
Please note that in this case JCMsuite is used in Daemon mode, allowing for parallel execution of the various wavelengths of the wavelength scan.
With appropriate hardware and license, all wavelength responses can be computed at the same time, allowing for fast computation of the whole parameter scan.
data_analysis/run_simulation.m [ASCII]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56
local_jcm_path = getenv('JCMROOT'); addpath(fullfile(local_jcm_path, 'ThirdPartySupport', 'Matlab')); jcmwave_startup; jcmwave_set_num_threads(1); jcmwave_daemon_shutdown(); jcmwave_daemon_add_workstation('Multiplicity', 2, 'NThreads', 1); % geometry keys.uol = 1.e-9; keys.radius_scatterer = 400.0; keys.contains_substrate = true; keys.offset_sphere = -10.0; % offset between sphere and substrate in uol % refractive indices keys.n_1 = 1.0; % background keys.n_2 = 3.0 + 0.1i; % sphere keys.n_3 = 1.5; % substrate % S&P plane waves incidence angle keys.theta = 20; keys.fem_degree = 3; keys.n_steps = 0; c0 = 299792458; mu0 = 4*pi*1e-7; eps0 = 1/(mu0*c0^2); Z0 = sqrt(mu0/eps0); geo_cross_section = pi*(keys.radius_scatterer*keys.uol)^2; p_in = 0.5*keys.n_1/Z0*geo_cross_section; % parameter scan job_ids = []; results = []; simulation_results = []; counter = 0; wavelengths = [400:2:600]*1e-9; for ii = 1:length(wavelengths) counter = counter + 1; keys.vacuum_wavelength = wavelengths(ii); job_ids(end + 1) = jcmwave_solve('project.jcmp', keys, 'workingdir', fullfile('tmp', ['s_' num2str(counter, '%05i')])); results(counter, 1) = keys.vacuum_wavelength; results(counter, 6) = keys.fem_degree; results(counter, 7) = keys.n_steps; end; [simulation_results, logs] = jcmwave_daemon_wait(job_ids); for ii = 1:length(job_ids) this_result = simulation_results{ii}; field_energy = cell2mat(this_result{2}.ElectricFieldEnergy); omega = 2*pi*c0/keys.vacuum_wavelength; absorption = -2*omega*imag(field_energy(2, :))/p_in; flux_scat = cell2mat(this_result{4}.ElectromagneticFieldEnergyFlux); scattering = sum(real(flux_scat), 1)/p_in; results(ii, 2:3) = absorption; results(ii, 4:5) = scattering; end filename = ['results_' datestr(now,'yyyymmdd_HHMMSS') '.txt']; save ('-ascii', '-double', filename, 'results'); copyfile(filename, 'results.txt'); display_results;
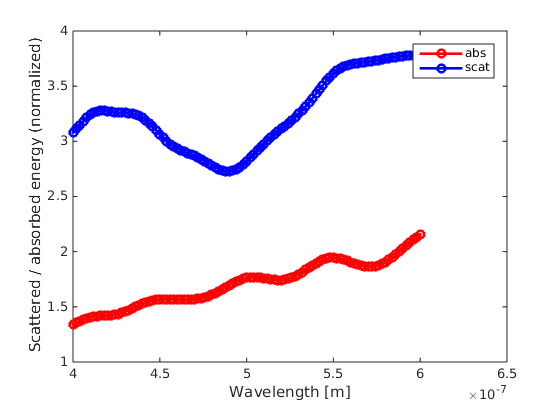
Wavelength-dependent absorption and scattering off a nanosphere on top of a substrate.¶