Derivatives (Sensitivities)¶

Derivative information of the goal functional with respect to input parameters are useful for studying the sensitivity of the output quantity under small perturbations of the input parameters. Furthermore, the most performance optimization and higher order interpolation require the computation of functional derivatives.

To support this, JCMsuite allows for the automatic computation of the derivatives. Furthermore, by using derivative information parameter scans can be accelerated by an higher order interpolation method.

This example demonstrates the computation of derivatives of the transmitted Fourier coefficients with respect to the plane wave illumination parameters 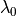$\lambda_0$ and the direction angles 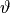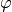$\vartheta$ , $\varphi$ , as well as with respect to the geometrical parameters (angles, width and height of the two triangular lines).

To define the illumination derivatives, remind that the sources.jcm input file has the data-tree like form

SourceBag {
  Source {
  ElectricFieldStrength {
    PlaneWave {
      Lambda0 = ...
      ThetaPhi = [...]
    }
  }
}

You can identify each input value by its tree path. For example the parameter Lambda0 within the PlaneWave section has the path SourceBag/Source/PlaneWave/Lambda0.

To activate automatic differentiation we declare derivative parameters at the beginning of the sources.jcm input file:

DerivativeParameter {
  Name = "Lambda0"
  TreeEntry = SourceBag/Source/ElectricFieldStrength/PlaneWave/Lambda0
  Scaling = 1e-9 # scale wavelength parameter in nanometer to have similar
                  # scaling of all derivative parameters
}

DerivativeParameter {
  Name = "Theta"
  TreeEntry = SourceBag/Source/ElectricFieldStrength/PlaneWave/ThetaPhi(1)
}

DerivativeParameter {
  Name = "Phi"
  TreeEntry = SourceBag/Source/ElectricFieldStrength/PlaneWave/ThetaPhi(2)
}

With a TreeEntry declaration we select a scalar input value for differentiation its tree path. The Name of the derivative parameters is used in the output files to refer to the specific derivative (see below for an usage within Matlab). A Scaling can be applied to account for a non-unitary influence on the input parameter.

Similarly, the layout.jcm input file has the data-tree like form

Layout2D {
  Objects {
    ...
    Triangle {
      Name = "Line1"
      DomainId = 3
      Height = 65.4
      Width = 200
      AngleAlpha = 65
      ...
    }
    ...
  }
}

The width of the first left triangle grating structure has the tree path Layout2D/Objects/Line1/Width (Here we used the Name Line1 instead of the section tag Triangle. This is allowed for named sections with a Name attribute).

To activate automatic differentiation we declare derivative parameters at the beginning of the layout.jcm input file:

DerivativeParameter {
 Name = "Height"
 TreeEntry = Layout2D/Objects/Line1/Height
}
DerivativeParameter {
 Name = "Width"
 TreeEntry = Layout2D/Objects/Line1/Width
}
DerivativeParameter {
 Name = "Alpha"
 TreeEntry = Layout2D/Objects/Line2/AngleAlpha
}
DerivativeParameter {
 Name = "Beta"
 TreeEntry = Layout2D/Objects/Line2/AngleBeta
}

Within Matlab, the table of the transmitted Fourier coefficients now comes with following additional columns containing the derivatives with respect to the seven parameters:

% primary Fourier coefficients of the two fields
ft_s = fourierTransform_transmitted.ElectricFieldStrength{1};
ft_p = fourierTransform_transmitted.ElectricFieldStrength{2};

% lambda0-derivatives of the Fourier coefficients of the two fields
dLambda0_ft_s =  fourierTransform_transmitted.d_Lambda0_ElectricFieldStrength{1};
dLambda0_ft_p =  fourierTransform_transmitted.d_Lambda0_ElectricFieldStrength{2};

% theta-derivatives of the Fourier coefficients of the two fields
dTheta_ft_s =  fourierTransform_transmitted.d_Theta_ElectricFieldStrength{1};
dTheta_ft_p =  fourierTransform_transmitted.d_Theta_ElectricFieldStrength{2};

% phi-derivatives of the Fourier coefficients of the two fields
dPhi_ft_s =  fourierTransform_transmitted.d_Phi_ElectricFieldStrength{1};
dPhi_ft_p =  fourierTransform_transmitted.d_Phi_ElectricFieldStrength{2};

% AngleAlpha-derivatives of the Fourier coefficients of the two fields
dAlpha_ft_s =  fourierTransform_transmitted.d_Alpha.ElectricFieldStrength{1};
dAlpha_ft_p =  fourierTransform_transmitted.d_Alpha.ElectricFieldStrength{2};

% AngleBeta-derivatives of the Fourier coefficients of the two fields
dBeta_ft_s =  fourierTransform_transmitted.d_Beta.ElectricFieldStrength{1};
dBeta_ft_p =  fourierTransform_transmitted.d_Beta.ElectricFieldStrength{2};

% Height-derivatives of the Fourier coefficients of the two fields
dHeight_ft_s =  fourierTransform_transmitted.d_Height.ElectricFieldStrength{1};
dHeight_ft_p =  fourierTransform_transmitted.d_Height.ElectricFieldStrength{2};

% Height-derivatives of the Fourier coefficients of the two fields
dWidth_ft_s =  fourierTransform_transmitted.d_Width.ElectricFieldStrength{1};
dWidth_ft_p =  fourierTransform_transmitted.d_Width.ElectricFieldStrength{2};

For demonstration purposes the script compare_diff_quotient.m compares the automatically computed derivatives with a numerical differentiation based on a difference quotient.

Note

The built-in automatic differentiation is faster and more accurate than the numerical differentiation based on difference quotients. This is especially evident from the Width derivative. Here, a small change has only a minuscule effect on the Fourier coefficients when computing difference quotients. Convergence of the difference quotients can be observed by using high precision settings and grid refinements, but at very high numerical costs.